(本小题满分14分)已知点列
 顺次为直线
顺次为直线 上的点,点列
上的点,点列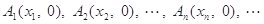
 顺次为
顺次为 轴上的点,其中
轴上的点,其中
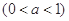 ,对任意的
,对任意的 ,点
,点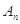 、
、 、
、 构成以
构成以 为顶点的等腰三角形.
为顶点的等腰三角形.
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)求证:对任意的 ,
, 是常数,并求数列
是常数,并求数列 的通项公式;
的通项公式;
(Ⅲ)试探究是否存在等腰直角三角形 ?并说明理由.
?并说明理由.
相关知识点
推荐套卷
(本小题满分14分)已知点列
 顺次为直线
顺次为直线 上的点,点列
上的点,点列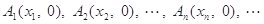
 顺次为
顺次为 轴上的点,其中
轴上的点,其中
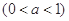 ,对任意的
,对任意的 ,点
,点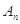 、
、 、
、 构成以
构成以 为顶点的等腰三角形.
为顶点的等腰三角形.
(Ⅰ)证明:数列 是等差数列;
是等差数列;
(Ⅱ)求证:对任意的 ,
, 是常数,并求数列
是常数,并求数列 的通项公式;
的通项公式;
(Ⅲ)试探究是否存在等腰直角三角形 ?并说明理由.
?并说明理由.