在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC =" AD" =" CD" =" DE" =2，AB =1．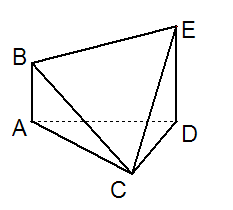
（1）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明你的结论；
（2）求多面体ABCDE的体积．
相关试题
的方程为
,试证明:坐标平面内任一点（
,在
）．若二次方程f（x）=0恰有两个不相等的实根x1和x2，求实数a的取值范围．
,在区间
上至少存在一个实数
使
,求实数
的取值范围.
，求
的最小值；
，若
有两个零点，求实数
的取值范围．推荐套卷
在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC =" AD" =" CD" =" DE" =2，AB =1．
（1）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明你的结论；
（2）求多面体ABCDE的体积．
粤公网安备 44130202000953号