如图,有一边长为5的正方形ABCD和等腰△PQR,PQ=PR=5cm,QR=8cm,点B,C,Q,R在同一条直线m上,当C,Q两点重合时,等腰△PQR以每秒1cm的速度沿直线m按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重合部分的面积为Scm2
(1) 当t =3秒时,设PQ与CD相交于点F,点E为QR的中点,连结PE求证:ΔQCF∽ΔQEP
(2)当t =6秒时,求S的值
(3)当8≤t≤13,求S关于t的函数解析式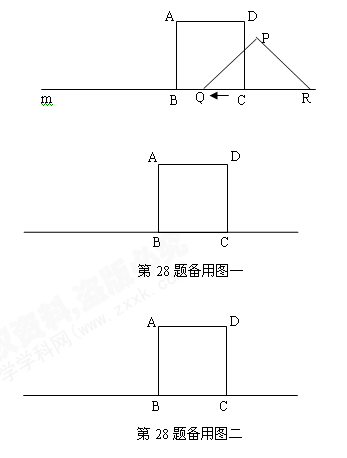
相关知识点
推荐套卷
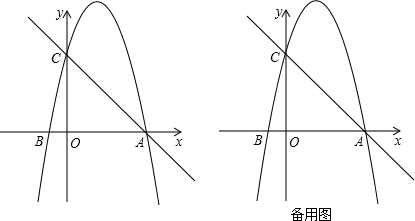
 (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
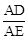 为定值;
为定值; 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0, 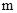 )作平行于
)作平行于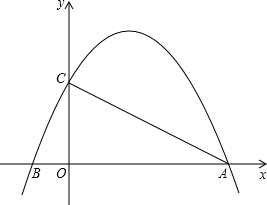
 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与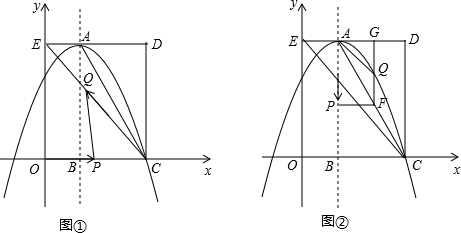
 粤公网安备 44130202000953号
粤公网安备 44130202000953号