（本小题满分12分）如图，等腰梯形ABCD的底边AB和CD长分别为6和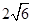
，高为3．
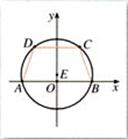
（1）求这个等腰梯形的外接圆E的方程；
（2）若线段MN的端点N的坐标为（5，2），端点M在圆E上运动，求线段MN的中点P的轨迹方程．
的通项
，求此数列的前
项和
.
.
中，
，求数列
的前
项和为
，已知
，设
，求数列
的通项公式．
中，
，求数列相关知识点
推荐套卷
（本小题满分12分）如图，等腰梯形ABCD的底边AB和CD长分别为6和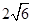，高为3．
（1）求这个等腰梯形的外接圆E的方程；
（2）若线段MN的端点N的坐标为（5，2），端点M在圆E上运动，求线段MN的中点P的轨迹方程．
粤公网安备 44130202000953号