某地区年降水量（单位：mm）在下列范围内的概率如下表：
| 年降水量 |
 |
 |
 |
 |
 |
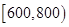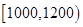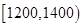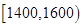| 概率 |
0．12 |
0．26 |
0．38 |
0．16 |
0．08 |
（1）如果降水量在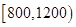
中，被认为是雨水适宜，有利于农作物生长，求该地区雨水适宜的概率；
（2）如果降水量不小于1200mm就可能发生洪涝灾害，这时需要采取防洪措施，求需要采取防洪措施的概率。
相关试题
；
．
是(1)实数；(2)纯虚数．
的三个内角
所对的边分别为
，向量
，
，且
．
的大小；
；②
；③
，试从中再选择两个条件以确定
图象的一部分如图所示．
的解析式；
时，求函数
的最大值与最小值及相应的
的值．
，求
的值；
，其中
为坐标原点，求
的值.推荐套卷
某地区年降水量（单位：mm）在下列范围内的概率如下表：
| 年降水量 |
|
|
|
|
|
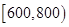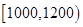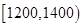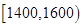| 概率 |
0．12 |
0．26 |
0．38 |
0．16 |
0．08 |
（1）如果降水量在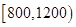中，被认为是雨水适宜，有利于农作物生长，求该地区雨水适宜的概率；
（2）如果降水量不小于1200mm就可能发生洪涝灾害，这时需要采取防洪措施，求需要采取防洪措施的概率。
粤公网安备 44130202000953号