(本小题满分14分)设函数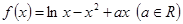 .
.
(1)求函数 的单调区间;
的单调区间;
(2)已知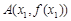 ,
,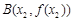 (
( )是函数
)是函数 在
在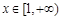 的图象上的任意两点,且满足
的图象上的任意两点,且满足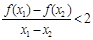 ,求a的最大值;
,求a的最大值;
(3)设 ,若对于任意给定的
,若对于任意给定的 ,方程
,方程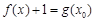 在
在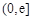 内有两个不同的实数根,求a的取值范围.(其中
内有两个不同的实数根,求a的取值范围.(其中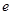 是自然对数的底数)
是自然对数的底数)
推荐套卷
(本小题满分14分)设函数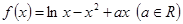 .
.
(1)求函数 的单调区间;
的单调区间;
(2)已知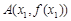 ,
,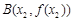 (
( )是函数
)是函数 在
在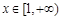 的图象上的任意两点,且满足
的图象上的任意两点,且满足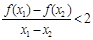 ,求a的最大值;
,求a的最大值;
(3)设 ,若对于任意给定的
,若对于任意给定的 ,方程
,方程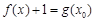 在
在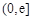 内有两个不同的实数根,求a的取值范围.(其中
内有两个不同的实数根,求a的取值范围.(其中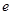 是自然对数的底数)
是自然对数的底数)