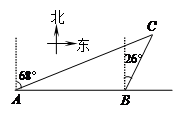（本题6分）一艘中国海监船自西向东航行，在A处测得钓鱼岛C在海监船的北偏东68°方向，继续向东航行80海里到达B处，此时测得钓鱼岛C在海监船的北偏东26°方向上．问：海监船再继续向东航行多少海里，距离钓鱼岛C最近？（结果保留整数）（参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.48，sin26°≈0.44，cos26°≈0.90，tan26°≈0.49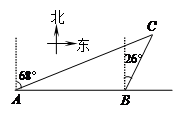）