已知直线l：mx﹣2y+2m=0（m∈R）和椭圆C：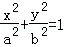
（a＞b＞0），椭圆C的离心率为
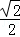，连接椭圆的四个顶点形成四边形的面积为2
．
（1）求椭圆C的方程；
（2）设直线l经过的定点为Q，过点Q作斜率为k的直线l′与椭圆C有两个不同的交点，求实数k的取值范围；
（3）设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f（m），求f（m）的表达式．
.
，求
的值；
对于
恒成立，求实数
的取值范围。
是定义在
上的增函数，且对一切
满足
.
的值;
解不等式
.
( a<0).
在
上是增函数;
取值范围.推荐套卷
已知直线l：mx﹣2y+2m=0（m∈R）和椭圆C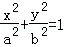：（a＞b＞0），椭圆C的离心率为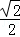，连接椭圆的四个顶点形成四边形的面积为2．
（1）求椭圆C的方程；
（2）设直线l经过的定点为Q，过点Q作斜率为k的直线l′与椭圆C有两个不同的交点，求实数k的取值范围；
（3）设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f（m），求f（m）的表达式．
粤公网安备 44130202000953号