在△ABC中，AB=AC，D是线段BC的延长线上一点，以AD为一边在AD的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．
（1）如图，点D在线段BC的延长线上移动，若∠BAC=40
,则∠DCE= ．
（2）设∠BAC=m，∠DCE=n．
①如图，当点D在线段BC的延长线上移动时，m与n之间有什么数量关系？请说明理由．
②当点D在直线BC上（不与B、C重合）移动时，m与n之间有什么数量关系？请直接写出你的结论．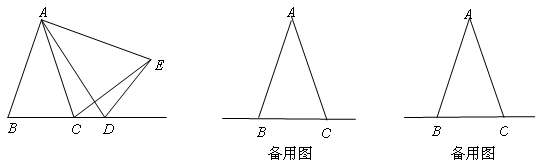
相关试题
，
时，求代数式
的值.
如图，抛物线
＝－
＋5
＋
经过点C（4，0），与轴交于另一点A，与轴交于点B．
（1）求点A、B的坐标；
（2）P是轴上一点，△PAB是等腰三角形，试求P点坐标；
（3）若·Q的半径为1，圆心Q在抛物线上运动，当·Q与轴相切时，求·Q上的点到点B的最短距离．
相关知识点
推荐套卷
粤公网安备 44130202000953号