为了考察冰川的融化状况,一支科考队在某冰川上相距8 km的A,B两点各建一个考察基地.视冰川面为平面形,以过A,B两点的直线为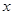 轴,线段AB的垂直平分线为
轴,线段AB的垂直平分线为 轴建立平面直角坐标系(如图).考察范围为到A,B两点的距离之和不超过10 km的区域.
轴建立平面直角坐标系(如图).考察范围为到A,B两点的距离之和不超过10 km的区域.
(1)求考察区域边界曲线的方程;
(2)如图所示,设线段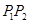 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?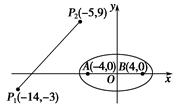
推荐套卷
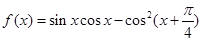 .
.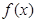 的单调区间;
的单调区间;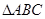 中,角
中,角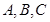 的对边分别为
的对边分别为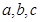 ,若
,若 ,求
,求 关于直线
关于直线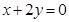 的对称点仍在圆上,且与直线
的对称点仍在圆上,且与直线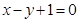 相交的弦长为
相交的弦长为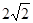 ,求圆的方程.
,求圆的方程. .
. ,求m的值.
,求m的值. 中,
中, =
= ,
, =1,
=1, 与平面
与平面 所成角的大小;
所成角的大小; 与平面
与平面 所成二面角的正弦值
所成二面角的正弦值 是正常数,
是正常数, ,
, ,求证:
,求证: ,指出等号成立的条件;
,指出等号成立的条件; (
( )的最小值,指出取最小值时
)的最小值,指出取最小值时 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号