某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。 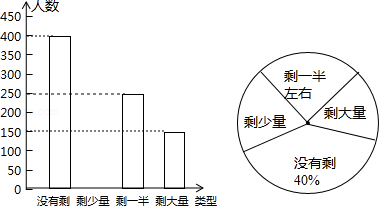
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
相关知识点
推荐套卷
 的顶点为D(﹣1,4),与
的顶点为D(﹣1,4),与 轴交于点C(0,3),与
轴交于点C(0,3),与 轴交于A,B两点(点A在点B的左侧)。
轴交于A,B两点(点A在点B的左侧)。
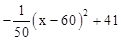 (万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入
(万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q=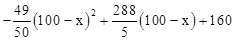 (万元)。
(万元)。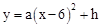 。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
。已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。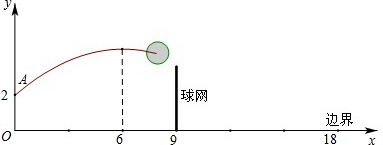
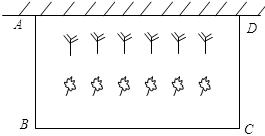
 ,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的
,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的 (m),花园的面积为
(m),花园的面积为 (m
(m ).
).
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量
 吗?若能,求出此时
吗?若能,求出此时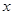 的值;若不能,说明理由;
的值;若不能,说明理由; 的图象交反比例函数
的图象交反比例函数 的图象于点A.B,交
的图象于点A.B,交 轴于点C。
轴于点C。
 的取值范围;
的取值范围;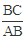 =
=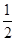 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号