对某校高一年级学生参加社区服务次数统计,随机抽去了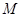 名学生作为样本,得到这
名学生作为样本,得到这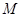 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
(1)求出表中 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选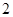 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间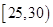 内的概率.
内的概率.
| 分组 |
频数 |
频率 |
 |
9 |
0.45 |
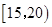 |
5 |
n |
 |
m |
r |
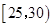 |
2 |
0.1 |
| 合计 |
M |
1 |
推荐套卷
 的参数方程是
的参数方程是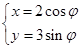 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线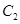 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在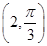 .
. 的取值范围.
的取值范围. 、
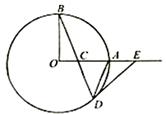
、 是圆
是圆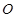 的半径,且
的半径,且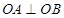 ,
, 是半径
是半径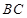 交圆
交圆 ,过
,过 .求证:
.求证: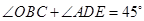 .
.
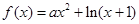 .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时,不等式
时,不等式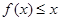 恒成立,求实数
恒成立,求实数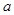 的取值范围.
的取值范围.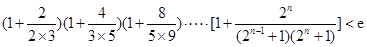 (
(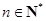 ,e是自然对数的底数).
,e是自然对数的底数). 的顶点为原点,其焦点
的顶点为原点,其焦点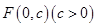 到直线
到直线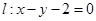 的距离为
的距离为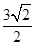 .设
.设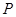 为直线
为直线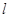 上的点,过点
上的点,过点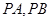 ,其中
,其中 为切点.
为切点.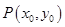 为直线
为直线 的方程;
的方程;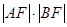 的最小值.
的最小值. 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.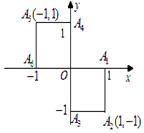
 粤公网安备 44130202000953号
粤公网安备 44130202000953号