如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AC=3CE时,求⊙O的半径.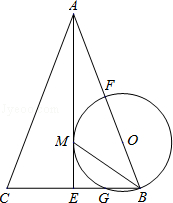
推荐套卷
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AC=3CE时,求⊙O的半径.