某学校在落实国家“营养餐”工程中,选用了 , , , 种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.
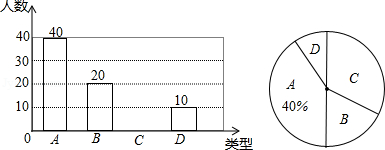
请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢 套餐的学生的人数.
推荐套卷
某学校在落实国家“营养餐”工程中,选用了 , , , 种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.

请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢 套餐的学生的人数.