在一次数学考试中,第22题和第23题为选做题.规定每位考生必须且只须在其中选做一题.设某4名考生选做每一道题的概率均为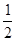 .
.
(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为 ,求
,求 的概率分布列及数学期望.
的概率分布列及数学期望.
推荐套卷
在一次数学考试中,第22题和第23题为选做题.规定每位考生必须且只须在其中选做一题.设某4名考生选做每一道题的概率均为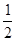 .
.
(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为 ,求
,求 的概率分布列及数学期望.
的概率分布列及数学期望.