已知圆 的方程为:
的方程为: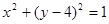 ,直线的方程为
,直线的方程为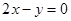 ,点
,点 在直线上,过点
在直线上,过点 作圆
作圆 的切线
的切线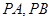 ,切点为
,切点为 .
.
(1)若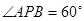 ,求点
,求点 的坐标;
的坐标;
(2)若点 的坐标为
的坐标为 ,过点
,过点 的直线与圆
的直线与圆 交于
交于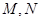 两点,当
两点,当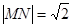 时,求直线
时,求直线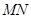 的方程;
的方程;
(3)求证:经过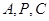 (其中点
(其中点 为圆
为圆 的圆心)三点的圆必经过定点,并求出所有定点的坐标.
的圆心)三点的圆必经过定点,并求出所有定点的坐标.
相关知识点
推荐套卷
已知圆 的方程为:
的方程为: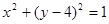 ,直线的方程为
,直线的方程为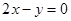 ,点
,点 在直线上,过点
在直线上,过点 作圆
作圆 的切线
的切线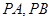 ,切点为
,切点为 .
.
(1)若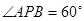 ,求点
,求点 的坐标;
的坐标;
(2)若点 的坐标为
的坐标为 ,过点
,过点 的直线与圆
的直线与圆 交于
交于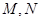 两点,当
两点,当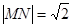 时,求直线
时,求直线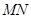 的方程;
的方程;
(3)求证:经过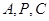 (其中点
(其中点 为圆
为圆 的圆心)三点的圆必经过定点,并求出所有定点的坐标.
的圆心)三点的圆必经过定点,并求出所有定点的坐标.