如图，一条直线与反比例函数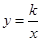
的图象交于A（1，4）
B（4，n）两点，与
轴交于D点，AC⊥轴，垂足为C．
（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；
（2）如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，直接写出F点坐标 ．
.
；
.
还少40º，求这个角.
一共要70元,买 
一共要50元.推荐套卷
如图，一条直线与反比例函数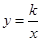的图象交于A（1，4）
B（4，n）两点，与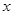轴交于D点，AC⊥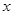轴，垂足为C．
（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；
（2）如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，直接写出F点坐标 ．
粤公网安备 44130202000953号