已知椭圆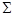 :
: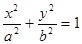 (
(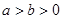 )的上顶点为
)的上顶点为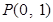 ,过
,过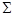 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为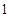 .若有一个菱形
.若有一个菱形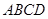 的顶点
的顶点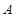 、
、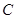 在椭圆
在椭圆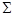 上,该菱形对角线
上,该菱形对角线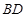 所在直线的斜率为
所在直线的斜率为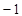 .
.
(1)求椭圆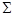 的方程;
的方程;
(2)当直线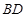 过点
过点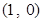 时,求直线
时,求直线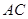 的方程;
的方程;
(3)当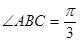 时,求菱形
时,求菱形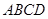 面积的最大值.
面积的最大值.
推荐套卷
已知椭圆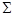 :
: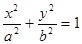 (
(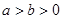 )的上顶点为
)的上顶点为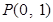 ,过
,过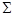 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为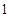 .若有一个菱形
.若有一个菱形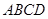 的顶点
的顶点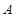 、
、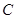 在椭圆
在椭圆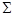 上,该菱形对角线
上,该菱形对角线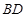 所在直线的斜率为
所在直线的斜率为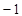 .
.
(1)求椭圆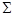 的方程;
的方程;
(2)当直线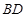 过点
过点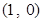 时,求直线
时,求直线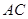 的方程;
的方程;
(3)当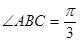 时,求菱形
时,求菱形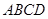 面积的最大值.
面积的最大值.