某学校对高一800名学生周末在家上网时间进行调查,抽取基中50个样本进行统计,发现上网的时间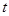 (小时)全部介于0至5之间.现将上网时间按如下方式分成五组:第一组
(小时)全部介于0至5之间.现将上网时间按如下方式分成五组:第一组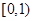 ,第二组
,第二组 ,第三组
,第三组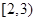 ,第四组
,第四组 ,第五组
,第五组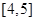 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.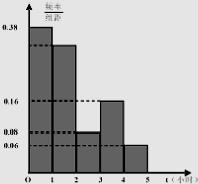
(1)求该样本中上网时间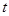 在
在 范围内的人数;
范围内的人数;
(2)请估计本年级800名学生中上网时间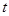 在
在 范围内的人数;
范围内的人数;
(3)若该样本中第三组只有两名女生,现从第三组中抽两名同学进行座谈,求抽到的两名同学恰好是一名男生和一名女生的概率.
推荐套卷
某学校对高一800名学生周末在家上网时间进行调查,抽取基中50个样本进行统计,发现上网的时间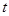 (小时)全部介于0至5之间.现将上网时间按如下方式分成五组:第一组
(小时)全部介于0至5之间.现将上网时间按如下方式分成五组:第一组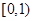 ,第二组
,第二组 ,第三组
,第三组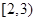 ,第四组
,第四组 ,第五组
,第五组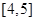 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)求该样本中上网时间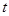 在
在 范围内的人数;
范围内的人数;
(2)请估计本年级800名学生中上网时间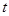 在
在 范围内的人数;
范围内的人数;
(3)若该样本中第三组只有两名女生,现从第三组中抽两名同学进行座谈,求抽到的两名同学恰好是一名男生和一名女生的概率.