如图,在平面直角坐标系中,抛物线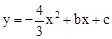 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.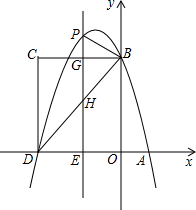
相关知识点
推荐套卷
 与
与 轴交于
轴交于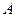 、
、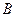 两点(点
两点(点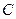 在第一象限,满足∠
在第一象限,满足∠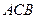 为直角,且恰使△
为直角,且恰使△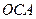 ∽△
∽△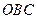 .
.
 的长.
的长. 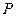 ,使△
,使△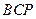 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的
 ,
, .
.
 ,求梯形ABCD的面积
,求梯形ABCD的面积

 粤公网安备 44130202000953号
粤公网安备 44130202000953号