如图，抛物线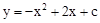与x轴交于A，B两点，它们的对称轴与x轴交于点N_优题课试题网

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 304

如图，抛物线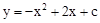与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.

登录免费查看答案和解析

相关试题

如图，△ABC是⊙O的内接三角形，AE是⊙O的直径，AF是⊙O的弦，且AF⊥BC于D点．

求证：（1）△ADC∽△ABE；
（2）BE＝CF．

题型：未知
难度：未知

收藏答案/解析

已知二次函数y＝ax²＋bx＋1的图像经过（1，2），（2，4）两点．
（1）求a、b值；（2）试判断该函数图像与x轴的交点情况，并说明理由．

题型：未知
难度：未知

收藏答案/解析

已知关于x的方程x²－6x＋m²－3m＝0的一根为2．
（1）求5m²－15m－100的值；
（2）求方程的另一根．

题型：未知
难度：未知

收藏答案/解析

如图，AC是△ABD的高，∠D＝45°，∠B＝60°，AD＝10．求AB的长．

题型：未知
难度：未知

收藏答案/解析

解方程：x²－6x－7＝0．

题型：未知
难度：未知

收藏答案/解析

相关知识点

相似多边形的性质二次函数在给定区间上的最值

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备

粤公网安备 44130202000953号

Copyright ©2020-2026 优题课 youtike.com 版权所有 Powered by：Youtike Platform 6.8.11

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。