如图，经过点A（0，﹣6）的抛物线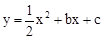
与x轴相交于B（﹣2，0），C两点．
（1）求此抛物线的函数关系式和顶点D的坐标；
（2）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m（m＞0）个单位长度得到新抛物线y1，若新抛物线y1的顶点P在△ABC内，求m的取值范围；
（3）在（2）的结论下，新抛物线y1上是否存在点Q，使得△QAB是以AB为底边的等腰三角形？请分析所有可能出现的情况，并直接写出相对应的m的取值范围．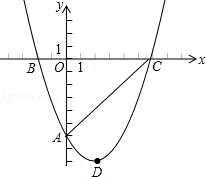
，完全燃烧1㎏煤却只能释放
的热，1㎏煤的全部能量是完全燃烧释放的热的多少倍？（保留3个有效数字）.
，
，
，试求
的值.
是36的平方根，
是
的立方根，
的算术平方根是3，求出
的值.
.
，其中
，
相关知识点
推荐套卷
如图，经过点A（0，﹣6）的抛物线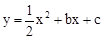与x轴相交于B（﹣2，0），C两点．
（1）求此抛物线的函数关系式和顶点D的坐标；
（2）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m（m＞0）个单位长度得到新抛物线y1，若新抛物线y1的顶点P在△ABC内，求m的取值范围；
（3）在（2）的结论下，新抛物线y1上是否存在点Q，使得△QAB是以AB为底边的等腰三角形？请分析所有可能出现的情况，并直接写出相对应的m的取值范围．
粤公网安备 44130202000953号