已知函数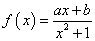
（其中常数
），
（ 
是圆周率）．
（1）当
时，若函数
是奇函数，求的极值点；
（2）当
时，求函数的单调递增区间；
（3）当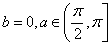
时，求函数
在
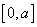上的最小值
，并探索：是否存在满足条件的实数
，使得对任意的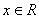
，
恒成立．
中，
，
，求证：
．
，
平面
，如图．求证：直线
与平面
相交．
平面
，
，
，△
的平面角的正切值为多少．
，
为不共面直线，
，
两点在
，
两点在
，
，如图所示．求证：直线
直线
推荐套卷
已知函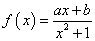数（其中常数），（ 是圆周率）．
（1）当时，若函数是奇函数，求的极值点；
（2）当时，求函数的单调递增区间；
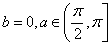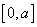（3）当时，求函数在上的最小值，并探索：是否存在满足条件的实数，使得对任意的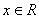，恒成立．
粤公网安备 44130202000953号