从某节能灯生产线上随机抽取100件产品进行寿命试验，按连续使用时间（单位：天）共分5组，得到频率分布直方图如图．
（1）请根据频率分布直方图，估算样本数据的众数和中位数（中位数精确到0．01）；
（2）若将频率视为概率，从该生产线所生产的产品（数量很多）中随机抽取3个，用ξ表示连续使用寿命高于350天的产品件数，求ξ的分布列和期望．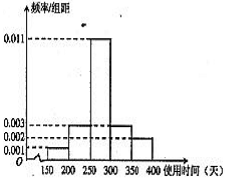
相关试题
，2kπ+π）（k∈Z），求角α的各三角函数值．
+lg（2cosx－1）的定义域．
；推荐套卷
从某节能灯生产线上随机抽取100件产品进行寿命试验，按连续使用时间（单位：天）共分5组，得到频率分布直方图如图．
（1）请根据频率分布直方图，估算样本数据的众数和中位数（中位数精确到0．01）；
（2）若将频率视为概率，从该生产线所生产的产品（数量很多）中随机抽取3个，用ξ表示连续使用寿命高于350天的产品件数，求ξ的分布列和期望．
粤公网安备 44130202000953号