某部门为了了解用电量
（单位：度）与气温x（单位：
）之间的关系，随机统计了某4天的用电量与当天气温，因某天统计的用电量数据丢失，用
表示，如下表：
| 气温（） |
18 |
13 |
10 |
-1 |
| 用电量（度） |
24 |
t |
38 |
64 |
（1）由以上数据，求这4天气温的方差 .
（2）若用电量与气温之间具有较好的线性相关关系，回归直线方程为
，且预测气温为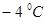
时，用电量为68度，求
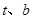的值.
推荐套卷
某部门为了了解用电量（单位：度）与气温x（单位：）之间的关系，随机统计了某4天的用电量与当天气温，因某天统计的用电量数据丢失，用表示，如下表：
| 气温（） |
18 |
13 |
10 |
-1 |
| 用电量（度） |
24 |
t |
38 |
64 |
（1）由以上数据，求这4天气温的方差 .
（2）若用电量与气温之间具有较好的线性相关关系，回归直线方程为，且预测气温为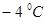时，用电量为68度，求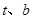的值.
粤公网安备 44130202000953号