如图,抛物线y=ax2+bx经过点A(4,0),B(2,2).连接OB,AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出△OA′B′的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.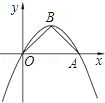
相关知识点
推荐套卷
如图,抛物线y=ax2+bx经过点A(4,0),B(2,2).连接OB,AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出△OA′B′的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.