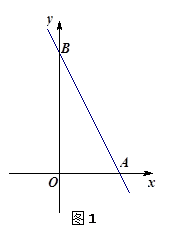
直线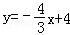 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?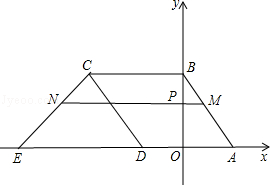
相关知识点
推荐套卷

 -
- )×
)×
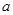 ,0),B(0,
,0),B(0,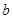 ),且
),且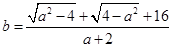 .
.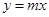 在第一象限上一点,且△ABM是等腰直角三角形,求
在第一象限上一点,且△ABM是等腰直角三角形,求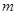 的值.
的值.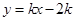 交
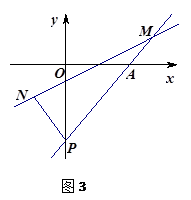
交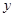 轴负半轴于点P,N点的横坐标为-1,过N点的直线
轴负半轴于点P,N点的横坐标为-1,过N点的直线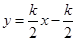 交AP于点M,给出两个结论:①
交AP于点M,给出两个结论:①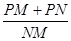 的值是不变;②
的值是不变;②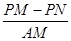 的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。
的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。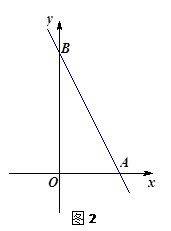
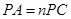 .
.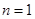 ,则
,则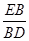 = ,
= ,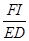 = ;
= ;
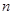 和
和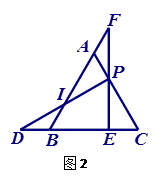
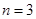 ,其他条件不变,则
,其他条件不变,则
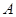 型产品40件,
型产品40件,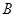 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表: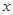 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为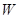 (元),求
(元),求 粤公网安备 44130202000953号
粤公网安备 44130202000953号