某人准备租一辆车从孝感出发去武汉，已知从出发点到目的地的距离为
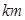，按交通法规定：这段公路车速限制在
（单位：
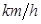）之间.假设目前油价为
（单位：元
），汽车的耗油率为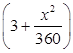
（单位：
）, 其中
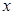（单位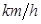：）为汽车的行驶速度，耗油率指汽车每小时的耗油量.租车需付给司机每小时的工资为
元，不考虑其它费用，这次租车的总费用最少是多少？此时的车速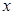是多少？（注：租车总费用=耗油费+司机的工资）
相关试题
(i为虚数单位)
是实数，且－1＜ω＜2
，求证：u为纯虚数；
，是否存在整式
，使得
对n≥2的一切自然数都成立?并试用数学
的展开式中，第6项与第7的系数相等,求展开式中二项式系数最大的项和系数最大的项．
求证:
推荐套卷
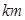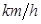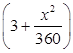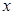某人准备租一辆车从孝感出发去武汉，已知从出发点到目的地的距离为，按交通法规定：这段公路车速限制在（单位：）之间.假设目前油价为（单位：元），汽车的耗油率为（单位：）, 其中（单位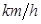：）为汽车的行驶速度，耗油率指汽车每小时的耗油量.租车需付给司机每小时的工资为元，不考虑其它费用，这次租车的总费用最少是多少？此时的车速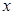是多少？（注：租车总费用=耗油费+司机的工资）
粤公网安备 44130202000953号