如图，顺达驾校拟在长为400m的道路OP的一侧修建一条训练道路，训练道路的前一部分为曲线段OSM，该曲线段为函数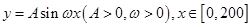
的图象，且图象的最高点为
，训练道路的后一部分为折线段MNP，为保证训练安全，限定
.
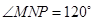（I）求曲线段OSM对应函数的解析式；
（II）应如何设计，才能使折线段训练道路MNP最长？最长为多少？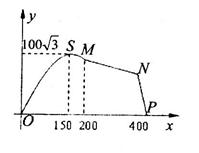
相关试题
.
的值域为
，求a的值；
上是增函数,求实数
的取值范围．
上的奇函数
，满足
，又当
时，
的取值范围。推荐套卷
如图，顺达驾校拟在长为400m的道路OP的一侧修建一条训练道路，训练道路的前一部分为曲线段OSM，该曲线段为函数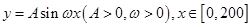的图象，且图象的最高点为，训练道路的后一部分为折线段MNP，为保证训练安全，限定.
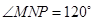（I）求曲线段OSM对应函数的解析式；
（II）应如何设计，才能使折线段训练道路MNP最长？最长为多少？
粤公网安备 44130202000953号