已知二次函数g(x)对任意x∈R都满足g(x-1)+g(1-x)=x2-2x-1且g(1)=-1，设函数f(x)=g(x+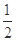
)+ m 
+
(m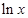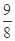∈R，x>0)．
(1)求g(x)的表达式；
(2)若存在x∈(0，+∞)，使f(x)≤0成立，求实数m的取值范围；
(3)设1<m≤e，H(x)=f(x)-(m+1)x，
求证：对于任意x1,x2∈［1,m］，恒有|H(x1)-H(x2)|<1.
是复数，
与
均为实数，且复数
在复平面上对应的点在第一象限，求实数
的取值范围．
=
.
时，求不等式 
的解集包含
，求
的取值范围.
推荐套卷
已知二次函数g(x)对任意x∈R都满足g(x-1)+g(1-x)=x2-2x-1且g(1)=-1，设函数f(x)=g(x+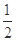)+ m 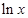+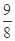(m∈R，x>0)．
(1)求g(x)的表达式；
(2)若存在x∈(0，+∞)，使f(x)≤0成立，求实数m的取值范围；
(3)设1<m≤e，H(x)=f(x)-(m+1)x，
求证：对于任意x1,x2∈［1,m］，恒有|H(x1)-H(x2)|<1.
粤公网安备 44130202000953号