(1)如图1,已知△ABC,以边AB、AC为边分别向外作等边三角形ABD和等边三角形ACE,连接CD、BE.求证:⑴CD=BE.
(2)如图2,已知△ABC,以边AB、AC为边分别向外作正方形ABFD和正方形ACGE,连接CD、BE,CD与BE有什么数量关系?(直接写结果,不需要过程).
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.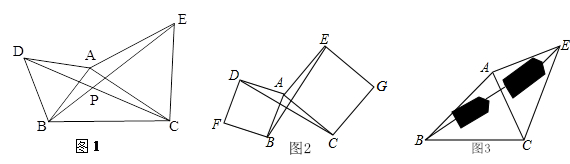
相关知识点
推荐套卷
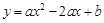 经过点
经过点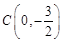 ,且与
,且与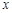 轴交于点
轴交于点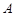 、点
、点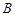 ,若
,若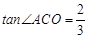 .
.
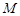 ,点
,点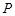 是线段
是线段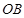 上一动点(不与点
上一动点(不与点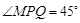 ,射线
,射线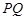 与线段
与线段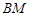 交于点
交于点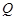 ,当△
,当△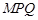 为等腰三角形时,求点
为等腰三角形时,求点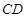 是△
是△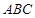 中
中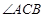 的角平分线,
的角平分线,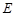 是
是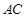 上的一点,且
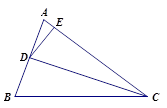
上的一点,且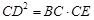 ,
,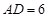 ,
,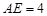 .
.
 ∽△
∽△ ;
;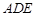 ∽△
∽△ ;
; 的长.
的长. ,在
,在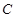 处测得楼顶
处测得楼顶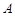 的仰角为30°,向高楼前进100米到达
的仰角为30°,向高楼前进100米到达 处,在
处,在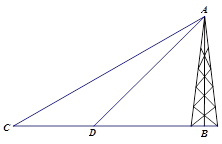
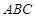 中,
中, ,
, ,点
,点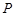 是△
是△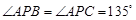 .
.
 ∽△
∽△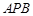 ;
;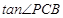 的值.
的值.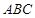 中,点
中,点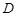 是
是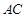 边上的一点,且
边上的一点,且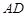 :
: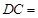 2:1.
2:1.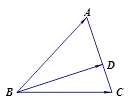
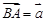 ,
, ,先化简,再求作:
,先化简,再求作: ;
;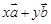 (
(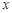 、
、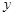 为实数)的形式表示
为实数)的形式表示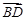 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号