如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m．经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），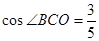
．以
所在直线为
轴，以
所在直线为
轴建立平面直角坐标系.
（Ⅰ）求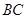
所在直线的方程及新桥BC的长；
（Ⅱ）当OM多长时，圆形保护区的面积最大？
并求此时圆的方程.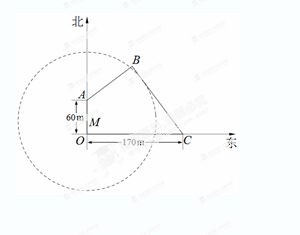
相关试题
.
的单调区间；
恒成立，求实数a的取值范围．
13分)设等差数列
满足
.
.
，且
为第一象限角，求y的值；
，求y的值．
在定义域
上是减函数，满足f(1-a)+f(1-
2a)〈0，求
的取值范围。
(a〉0,且a≠1)在区间[1,2]上的最大值比最小值大
，求a的值
。相关知识点
推荐套卷
粤公网安备 44130202000953号