已知抛物线y=x2﹣(k+2)x+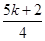 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,直线AD交直线CE于点G(如图),且CA•GE=CG•AB,求抛物线的解析式.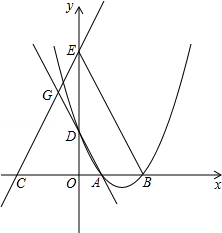
相关知识点
推荐套卷
 ,∠ABC=
,∠ABC= ,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是
,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是 .
.


 角(
角( 且
且 ,
, 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,连接BE.
边于点E,连接BE.

 与⊙E的位置关系.
与⊙E的位置关系. (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0). 与此抛物线的另一个交点为
与此抛物线的另一个交点为 ,
, ,求点P的坐标;
,求点P的坐标;  (n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .
(n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .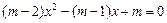 .(其中m为实数)
.(其中m为实数)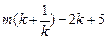 为y,求y与m的关系式;
为y,求y与m的关系式;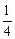 <m<2时,判断此方程的实数根的个数并说明理由
<m<2时,判断此方程的实数根的个数并说明理由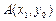 ,
,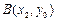 是抛物线
是抛物线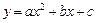 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线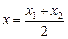 为此抛物线的对称轴.
为此抛物线的对称轴.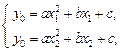 且
且
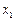 ≠
≠
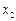 .
.
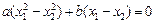 .
.
 .
.
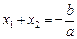 .
.
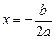 ,
,
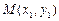 ,
,
 是抛物线
是抛物线
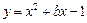 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号