在△ABC和△DEF中，∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤，其正面分别写有五个不同的等式，小民将这五张纸牌背面朝上洗匀后先随机摸出一张（不放回），再随机摸出一张．请结合以上条件，解答下列问题．
（1）、你认为 和 组合，△ABC和△DEF不一定全等，
（2）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用①、②、③、④、⑤表示）；
（3）用两次摸牌的结果和∠C=∠F=90°作为条件，求能满足△ABC和△DEF全等的概率．
相关试题
．列方程解应用题：
小明和小东两人练习跑步，都从甲地出发跑到乙地，小明每分钟跑250米，小东每分钟跑200米，小明让小东先出发3分钟之后再出发，结果两人同时到达乙地，求甲、乙两地之间的路程是多少米？
，求代数式
的值．
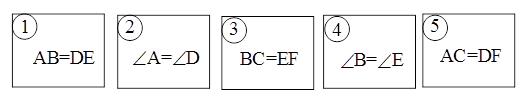
为抛物线“y1＝4x2＋b1x＋c1”，其他条件不变，求b1＋b2的值▲（直接写结果）．相关知识点
推荐套卷
粤公网安备 44130202000953号