如图，梯形ABCD中，AB∥CD，AC⊥BD于点0，∠CDB=∠CAB，DE⊥AB，CF⊥AB，E．F为垂足．设DC=m，AB=n．（1）求证：△ACB≌△BDA；（2）求四边形DEFC的周长．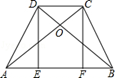
并写出其所有自然数解
．
是直角三角形，
，点
的坐标分别为
，
的直线的函数表达式
轴上找一点
，连接
，使得
与
分别是
和
上的动点，连接
，设
，问是否存在这样的
使得
与相关知识点
推荐套卷
如图，梯形ABCD中，AB∥CD，AC⊥BD于点0，∠CDB=∠CAB，DE⊥AB，CF⊥AB，E．F为垂足．设DC=m，AB=n．（1）求证：△ACB≌△BDA；（2）求四边形DEFC的周长．
粤公网安备 44130202000953号