如图,点A,B分别在 轴,
轴,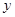 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥ 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA=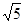 ,反比例函数
,反比例函数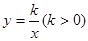 的图象过CD的中点E。
的图象过CD的中点E。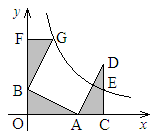
(1)求证:△AOB≌△DCA;
(2)求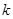 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在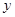 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
相关知识点
推荐套卷
如图,点A,B分别在 轴,
轴,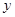 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥ 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA=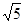 ,反比例函数
,反比例函数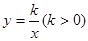 的图象过CD的中点E。
的图象过CD的中点E。
(1)求证:△AOB≌△DCA;
(2)求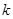 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(