已知函数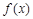
满足2
+
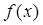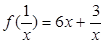，对x≠0恒成立，在数列{an}、{bn}中，a1=1，b1=1，对任意x∈N+，
，
。
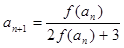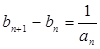（1）求函数
解析式；
（2）求数列{an}、{bn}的通项公式；
（3）若对任意实数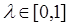
,总存在自然数k,当n≥k时,
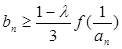恒成立，求k的最小值。
相关试题
，命题“
”为真，“
”为真，求实数
的取值范围．
，求函数
在点
处的切线方程．
．
时，求函数
的单调区间；
时，令
．求
在
上的最大值和最小值；
对
恒成立，求实数
的取值范围
上任意一点到两焦点
距离之和为
，离心率为
．
的斜率为
，直线
两点．点
为椭圆上一点，求
的面积的最大值．
的一元二次方程
，其中
．若
随机选自区间
，
随机选自区间
，求方程有实根的概率．推荐套卷
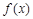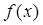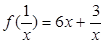已知函数满足2+，对x≠0恒成立，在数列{an}、{bn}中，a1=1，b1=1，对任意x∈N+，，。
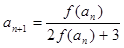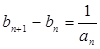（1）求函数解析式；
（2）求数列{an}、{bn}的通项公式；
（3）若对任意实数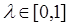,总存在自然数k,当n≥k时,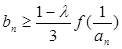恒成立，求k的最小值。
粤公网安备 44130202000953号