某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是
,
,
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin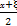
π(x∈R)是偶函数”为事件D,求事件D发生的概率.
及
，对角线的交点是
，求另两边所在直线的方程．
+
+
≥
+
+
．
相交于点M，在OM上取一点P，使得
，求点P的轨迹的极坐标方程．
。
，若
所对应的变换
把直线
变换为自身，求实数
，并求M的逆矩阵．推荐套卷
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是,,且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin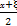π(x∈R)是偶函数”为事件D,求事件D发生的概率.
粤公网安备 44130202000953号