如图所示，n台机器人M1，M2，……，Mn位于一条直线上，检测台M在线段M1 Mn上，n台机器人需把各自生产的零件送交M处进行检测，送检程序设定：当Mi把零件送达M处时，Mi+1即刻自动出发送检（i=1,2,……,n-1）已知Mi的送检速度为V(V>0), 且
记
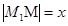，n台机器人送检时间总和为f(x).
 |
(1)求f(x)的表达式；
(2)当n=3时，求x的值使得f(x)取得最小值；
(3)求f(x)取得最小值时，x的取值范围．
＋
＋
的最大值．
与
的大小．
(a>0)对应的变换作用下得到的曲线为x2＋y2＝1.
，B＝
，求矩阵A－1B.
，求矩阵A的特征值．推荐套卷
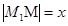如图所示，n台机器人M1，M2，……，Mn位于一条直线上，检测台M在线段M1 Mn上，n台机器人需把各自生产的零件送交M处进行检测，送检程序设定：当Mi把零件送达M处时，Mi+1即刻自动出发送检（i=1,2,……,n-1）已知Mi的送检速度为V(V>0), 且记，n台机器人送检时间总和为f(x).
|
(1)求f(x)的表达式；
(2)当n=3时，求x的值使得f(x)取得最小值；
(3)求f(x)取得最小值时，x的取值范围．
粤公网安备 44130202000953号