四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF，连接DF，G为DF的中点，连接EG，CG，EC．
（1）如图1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及
的值；
（2）将图1中的△BEF绕点B顺时针旋转至图2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；
（3）将图1中的△BEF绕点B顺时针旋转α（0°＜α＜90°），若BE=1，
，当E，F，D三点共线时，求DF的长及tan∠ABF的值．
相关试题
－1)0－32＋
已知点O到△ABC的两边AB、AC所在直线的距离相等，且OB=OC如图16，若点O在BC上，求证AB=AC。
如图17，若点O在△ABC内部，求证AB=AC。
猜想，若O点在△ABC的外部，AB=AC成立吗？
相关知识点
推荐套卷
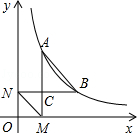
粤公网安备 44130202000953号