在某校八(1)班组织了无锡欢乐义工活动,就该班同学参与公益活动情况作了一次调查统计.如图是一同学通过收集数据后绘制的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)该班共有______名学生,其中经常参加公益活动的有_____名学生;
(2)将频数分布直方图补充完整;
(3)若该校八年级有600名学生,试估计该年级从不参加的人数.若我市八年级有21000名学生,能否由此估计出我市八年级学生从不参加的人数,为什么?
(4)根据统计数据,你想对你的同学们说些什么?
相关知识点
推荐套卷
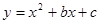 过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.
过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.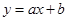 的图象与反比例函数
的图象与反比例函数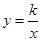 的图象交于A(1,4)、B(﹣2,m)两点,
的图象交于A(1,4)、B(﹣2,m)两点, 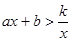 的解集.
的解集.
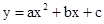 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交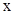 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.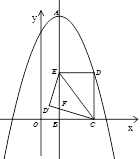
 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标; 粤公网安备 44130202000953号
粤公网安备 44130202000953号