如图,在平面直角坐标系中,抛物线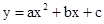 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.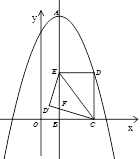
(1)求抛物线的解析式;
(2)若点D′恰好落在 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标;
(3)直线CD′交对称轴AB于点F,
①当点D′在对称轴AB的左侧时,且△ED′F∽△CDE,求出DE:DC的值;
②连结B D′,是否存在点E,使△E D′B为等腰三角形?若存在,请直接写出BE:BC的值,若不存在请说明理由.
相关知识点
推荐套卷
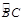 和弦AC的长. (弧长计算结果保留
和弦AC的长. (弧长计算结果保留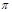 ,弦长精确到0.01)
,弦长精确到0.01)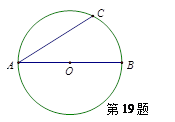

 粤公网安备 44130202000953号
粤公网安备 44130202000953号