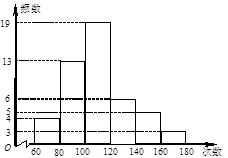
某中学对全校学生1分钟跳绳的次数进行了统计，全校1分钟跳绳的平均次数是100次．某班体育委员统计了全班50名学生1分钟跳绳的成绩，列出的频数分布直方图如下（每个分组包括左端点，不包括右端点）．
（1）求该班学生中跳绳次数达到或超过校平均水平的占全班人数的百分比；
（2）该班1分钟跳绳的平均次数至少是多少？是否超过全校平均次数？
（3）已知该班成绩最好的三名学生中有一名男生和两名女生，现要从三人中随机抽取两人参加学校举行的跳绳比赛，用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率．