阅读一段文字,再回答下列问题:已知在平面内两点的坐标为P1(x1,y1),P2(x2,y2),则该两点间距离公式为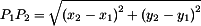 .同时,当两点在同一坐标轴上或所在直线平行于x轴、垂直于x轴时,两点间的距离公式可化简成|x2-x1|或|y2-y1|.
.同时,当两点在同一坐标轴上或所在直线平行于x轴、垂直于x轴时,两点间的距离公式可化简成|x2-x1|或|y2-y1|.
(1)若已知两点A(3,3),B(-2,-1),试求A,B两点间的距离;
(2)已知点M,N在平行于y轴的直线上,点M的纵坐标为7,点N的纵坐标为-2,试求M,N两点间的距离;
(3)已知一个三角形各顶点的坐标为A(0,5),B(-3,2),C(3,2),你能判定此三角形的形状吗?试说明理由.