甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
填写下表:
| |
平均数 |
众数 |
中位数 |
方差 |
| 甲 |
8 |
? |
8 |
0.4 |
| 乙 |
? |
9 |
? |
3.2 |
教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
相关知识点
推荐套卷
 条直线最少可以把平面分成几部分?最多可以把平面分成几部分?
条直线最少可以把平面分成几部分?最多可以把平面分成几部分?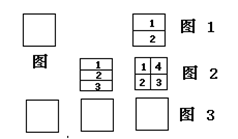
 在平面直角坐标系中.
在平面直角坐标系中. ;
; ,请你画出
,请你画出
 、
、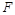 分别是
分别是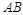 、
、 上一点,
上一点, ,
, 与
与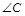 互余,
互余,  .
.


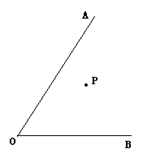
 为
为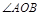 内部一点,过点
内部一点,过点 交
交 于
于 ,画垂线段
,画垂线段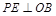 ,垂足为
,垂足为
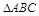 沿箭头的方向平移
沿箭头的方向平移

 粤公网安备 44130202000953号
粤公网安备 44130202000953号