如图，正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB//CD，AB=AD=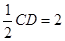
，点M在线段EC上且不与E、C垂合.
（1）当点M是EC中点时，求证：BM//平面ADEF；
（2）当平面BDM与平面ABF所成锐二面角的余弦值为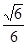
时，求三棱锥M—BDE的体积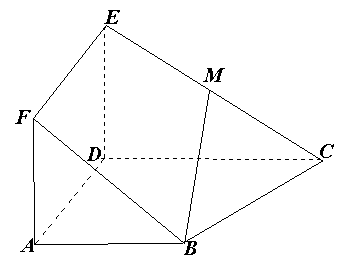
，
，
，
．当
，
，
，
时，分别求点
的坐标．
的边长为１，
，
分别为边
，
上的点．当
的周长为２时，求
的大小．
，
是
，
之间的一定点，并且
，
．
是直线
．且使
与直线
，求
面积的最小值．
，
，求
的值．
，试用含
的式子表示
．相关知识点
推荐套卷
如图，正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB//CD，AB=AD=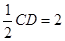，点M在线段EC上且不与E、C垂合.
（1）当点M是EC中点时，求证：BM//平面ADEF；
（2）当平面BDM与平面ABF所成锐二面角的余弦值为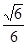时，求三棱锥M—BDE的体积
粤公网安备 44130202000953号