已知曲线C上的动点P（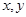
）满足到定点A(-1,0)的距离与到定点B（1,0）距离之比为
．
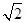（1）求曲线C的方程．
（2）过点M(1,2)的直线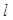
与曲线C交于两点M、N，若|MN|=4，求直线
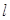的方程．
,则
.
求A;
求
的值.
,若
求实数
的值.
，集合
，
；
，求
的值。
，
，
满足
，
求实数
的值。相关知识点
推荐套卷
已知曲线C上的动点P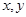（）满足到定点A(-1,0)的距离与到定点B（1,0）距离之比为．
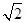（1）求曲线C的方程．
（2）过点M(1,2)的直线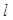与曲线C交于两点M、N，若|MN|=4，求直线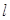的方程．
粤公网安备 44130202000953号