已知曲线C1：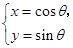
（
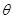为参数），曲线C2：
（t为参数）．
（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；
（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线
．写出的参数方程．
与
公共点的个数和C
公共点的个数是否相同？说明你的理由．
相关试题
是圆
内两弦
和
的交点，过
延长线上一点
作圆
，
为切点，已知
．求证：
∽
；
∥
．
。
与
在公共点
处有相同的切线，求实数
的值；
，求方程
在区间
内实根的个数（
为自然对数的底数）.
和动圆
，直线：
与
和
分别有唯一的公共点
和
．
的取值范围；
的最大值，并求此时圆
中，
，
平面
，
为
的中点，
，
．
；
为
的中点，求证：平面
平面
．
之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份的分数在
之间的概率；相关知识点
推荐套卷
已知曲线C1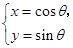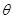：（为参数），曲线C2：（t为参数）．
（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；
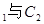（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线．写出的参数方程．与公共点的个数和C公共点的个数是否相同？说明你的理由．
粤公网安备 44130202000953号