某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由散点图可知,销售量 与价格
与价格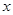 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;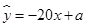
(1)求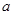 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)
推荐套卷
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由散点图可知,销售量 与价格
与价格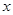 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;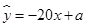
(1)求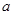 的值;
的值;
(2)预计在今后的销售中,销量与单价仍然服从线性回归直线方程中的关系,且该产品的成本是每件4元,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入一成本)