直线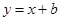 与
与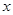 轴交于点C(4,0),与
轴交于点C(4,0),与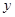 轴交于点B,并与双曲线
轴交于点B,并与双曲线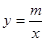
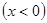 交于点
交于点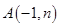 。
。
(1)求直线与双曲线的解析式。
(2)连接OA,求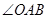 的正弦值。
的正弦值。
(3)若点D在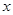 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。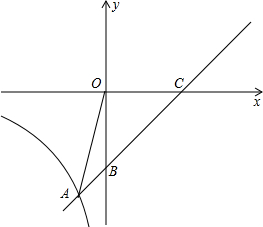
推荐套卷
直线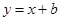 与
与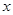 轴交于点C(4,0),与
轴交于点C(4,0),与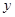 轴交于点B,并与双曲线
轴交于点B,并与双曲线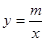
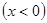 交于点
交于点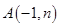 。
。
(1)求直线与双曲线的解析式。
(2)连接OA,求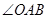 的正弦值。
的正弦值。
(3)若点D在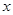 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。